Linear_Feedback_Shift_Register

LFSR -Linear Feedback Shift Register

Homepage

Links: Github Page | Documentation | Github | PyPi - project | _ Installation: pip install pylfsr

---

---

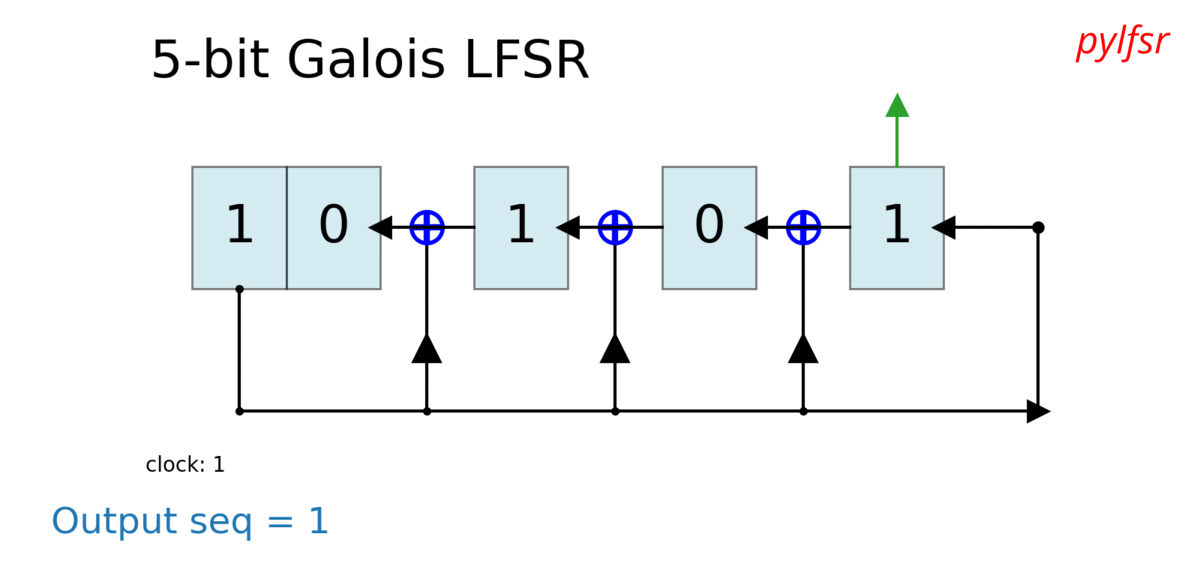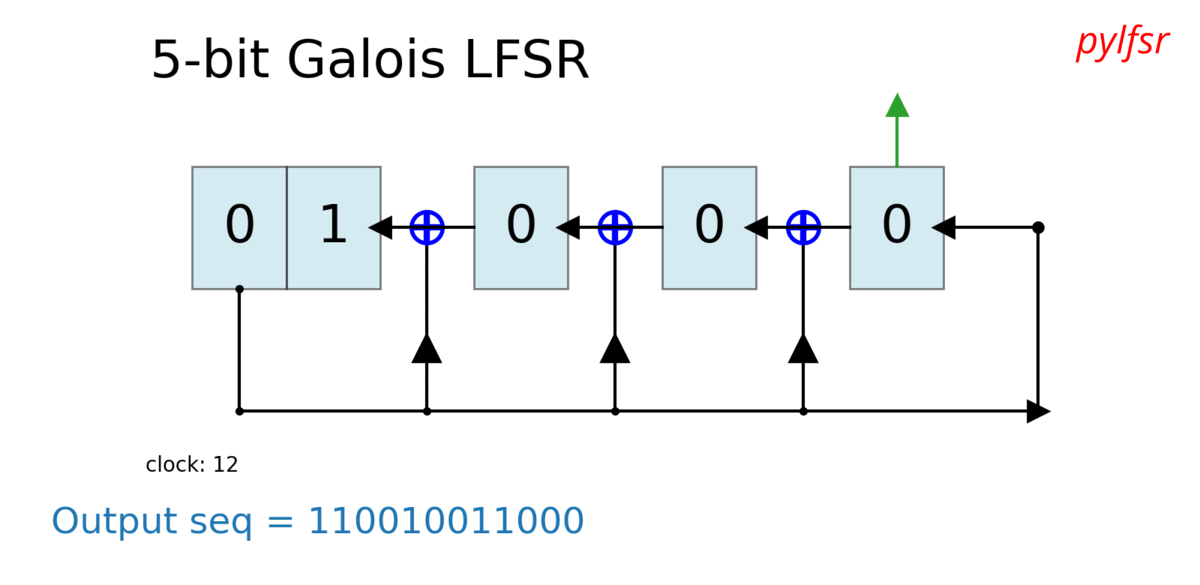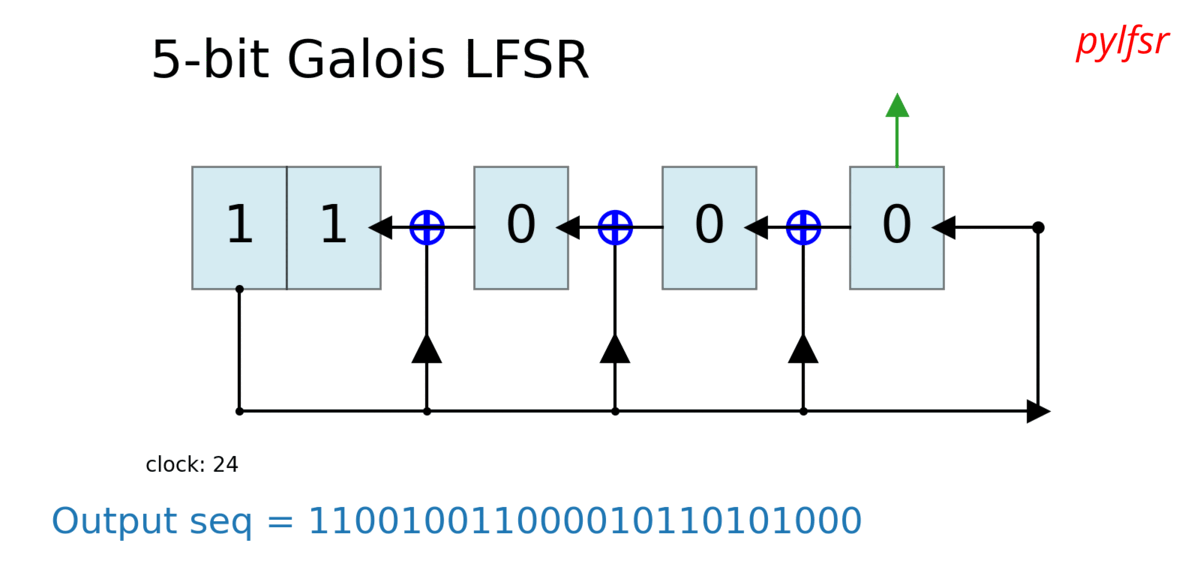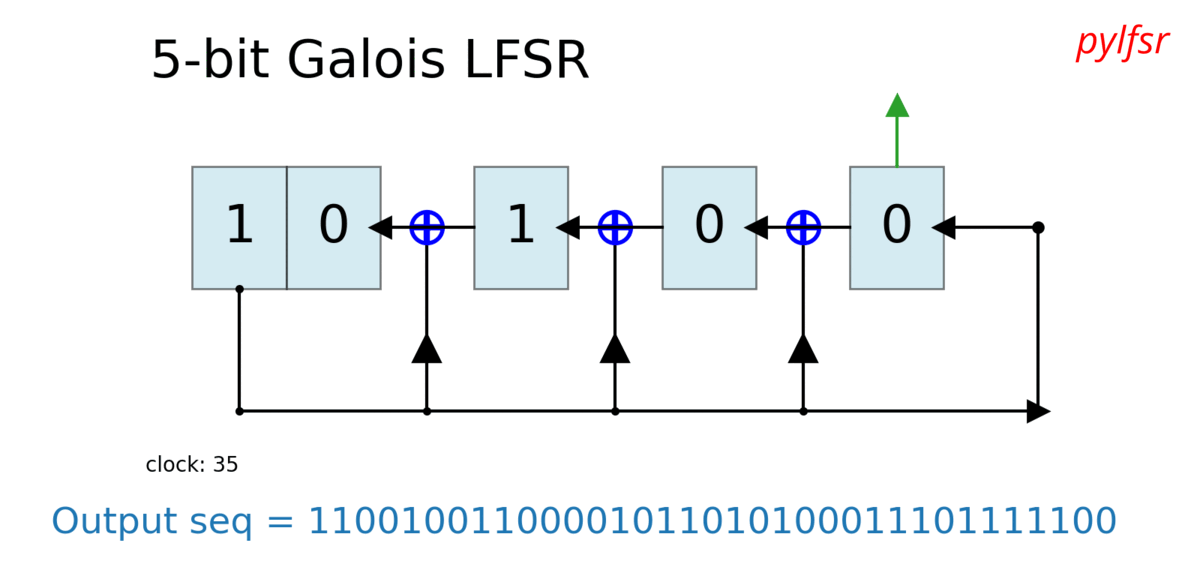
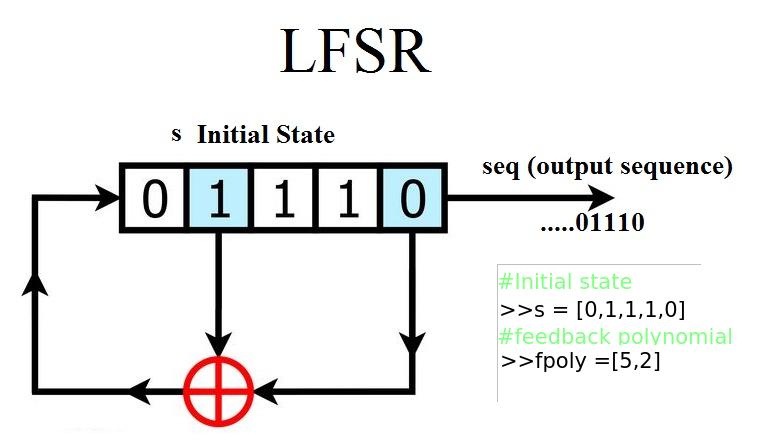
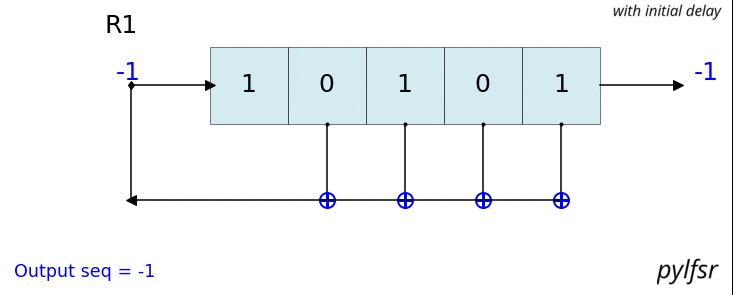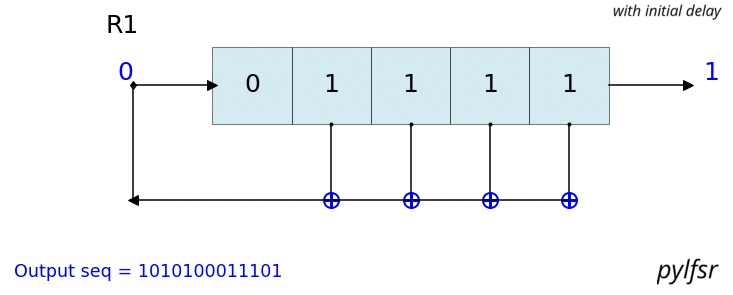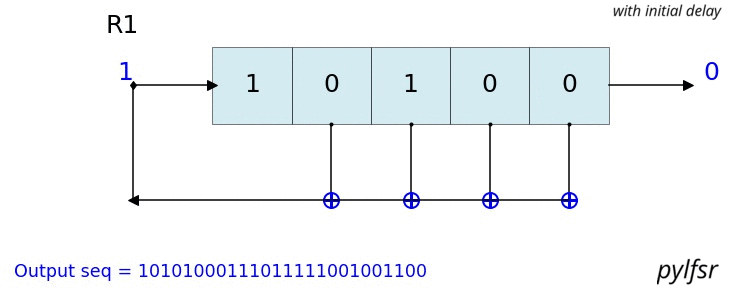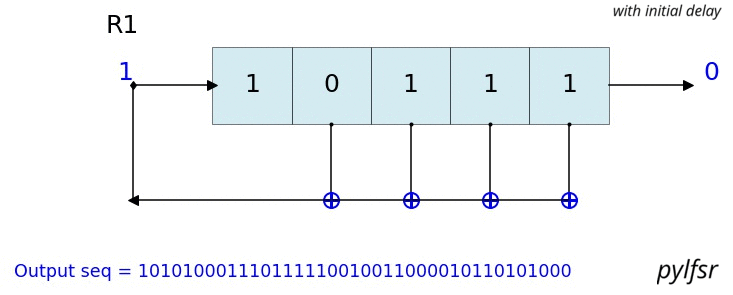
Table of contents

• New Updates
• Installation
• Examples
  • 5-bit LFSR
  • Vizualize each state
  • Plot your LFSR
  • Test properties of LFSR
• A5/1 GSM Stream Cipher
• Geffe Genegerator
• Matlab Implementation

• Cite As

New Updates

Plot Your LFSR with pylfsr

Updates:

Version: 1.0.7:

• Added Galois Configuration
• Improved Documentation
• Computing LZ complexity

Version: 1.0.6:

• Fixed the bugs (1) missing initial bit (2) exception
• Added test properties of LFSR
  • (1) Balance Property
  • (2) Runlength Property
  • (3) Autocorrelation Property
• Ploting function to display LFSR
• A5/1 GSM Stream Ciper Generator
• Geffe Generator

Installation

Requirement : numpy, matplotlib

with pip

pip install pylfsr

conda

conda install -c nikeshbajaj pylfsr

in process of including in conda-forge

Build from the source

Download the repository or clone it with git, after cd in directory build it from source with

python setup.py install

Examples

Example 1: 5-bit LFSR with feedback polynomial x^5 + x^2 + 1

# import LFSR
import numpy as np
from pylfsr import LFSR

L = LFSR()

# print the info
L.info()

5 bit LFSR with feedback polynomial  x^5 + x^2 + 1
Expected Period (if polynomial is primitive) =  31
Current :
State        :  [1 1 1 1 1]
Count        :  0
Output bit   : -1
feedback bit : -1

L.next()
L.runKCycle(10)
L.runFullCycle()
L.info()

Example 2**: 5-bit LFSR with custum state and feedback polynomial

state = [0,0,0,1,0]
fpoly = [5,4,3,2]
L = LFSR(fpoly=fpoly,initstate =state, verbose=True)
L.info()
tempseq = L.runKCycle(10)
L.set(fpoly=[5,3])

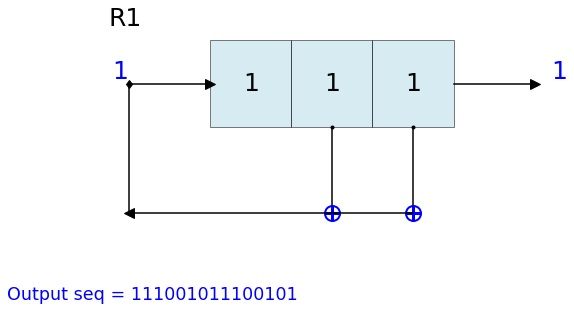
Example 3 ## To visualize the process with 3-bit LFSR, with default counter_start_zero = True

state = [1,1,1]
fpoly = [3,2]
L = LFSR(initstate=state,fpoly=fpoly)
print('count \t state \t\toutbit \t seq')
print('-'*50)
for _ in range(15):
    print(L.count,L.state,'',L.outbit,L.seq,sep='\t')
    L.next()
print('-'*50)
print('Output: ',L.seq)

Output :

count 	        state 		outbit 	 seq
--------------------------------------------------
0		[1 1 1]		-1	[-1]
1		[0 1 1]		1	[1]
2		[0 0 1]		1	[1 1]
3		[1 0 0]		1	[1 1 1]
4		[0 1 0]		0	[1 1 1 0]
5		[1 0 1]		0	[1 1 1 0 0]
6		[1 1 0]		1	[1 1 1 0 0 1]
7		[1 1 1]		0	[1 1 1 0 0 1 0]
8		[0 1 1]		1	[1 1 1 0 0 1 0 1]
9		[0 0 1]		1	[1 1 1 0 0 1 0 1 1]
10		[1 0 0]		1	[1 1 1 0 0 1 0 1 1 1]
11		[0 1 0]		0	[1 1 1 0 0 1 0 1 1 1 0]
12		[1 0 1]		0	[1 1 1 0 0 1 0 1 1 1 0 0]
13		[1 1 0]		1	[1 1 1 0 0 1 0 1 1 1 0 0 1]
14		[1 1 1]		0	[1 1 1 0 0 1 0 1 1 1 0 0 1 0]
--------------------------------------------------
Output:  [1 1 1 0 0 1 0 1 1 1 0 0 1 0 1]

Example 4 ## To visualize the process with 3-bit LFSR, with default counter_start_zero = False

state = [1,1,1]
fpoly = [3,2]
L = LFSR(initstate=state,fpoly=fpoly,counter_start_zero=False)
print('count \t state \t\toutbit \t seq')
print('-'*50)
for _ in range(15):
    print(L.count,L.state,'',L.outbit,L.seq,sep='\t')
    L.next()
print('-'*50)
print('Output: ',L.seq)

Output

count 	 state 		outbit 	 seq
--------------------------------------------------
1	[1 1 1]		1	[1]
2	[0 1 1]		1	[1 1]
3	[0 0 1]		1	[1 1 1]
4	[1 0 0]		0	[1 1 1 0]
5	[0 1 0]		0	[1 1 1 0 0]
6	[1 0 1]		1	[1 1 1 0 0 1]
7	[1 1 0]		0	[1 1 1 0 0 1 0]
8	[1 1 1]		1	[1 1 1 0 0 1 0 1]
9	[0 1 1]		1	[1 1 1 0 0 1 0 1 1]
10	[0 0 1]		1	[1 1 1 0 0 1 0 1 1 1]
11	[1 0 0]		0	[1 1 1 0 0 1 0 1 1 1 0]
12	[0 1 0]		0	[1 1 1 0 0 1 0 1 1 1 0 0]
13	[1 0 1]		1	[1 1 1 0 0 1 0 1 1 1 0 0 1]
14	[1 1 0]		0	[1 1 1 0 0 1 0 1 1 1 0 0 1 0]
--------------------------------------------------
Output:  [1 1 1 0 0 1 0 1 1 1 0 0 1 0 1]

Visualize & Plot LFSR

L.Viz(show=False, show_labels=False,title='R1')

Dynamic plot - Animation in notebook

%matplotlib notebook
L = LFSR(initstate=[1,0,1,0,1],fpoly=[5,4,3,2],counter_start_zero=False)
fig, ax = plt.subplots(figsize=(8,3))
for _ in range(35):
  ax.clear()
  L.Viz(ax=ax, title='R1')
  plt.ylim([-0.1,None])
  #plt.tight_layout()
  L.next()
  fig.canvas.draw()
  plt.pause(0.1)

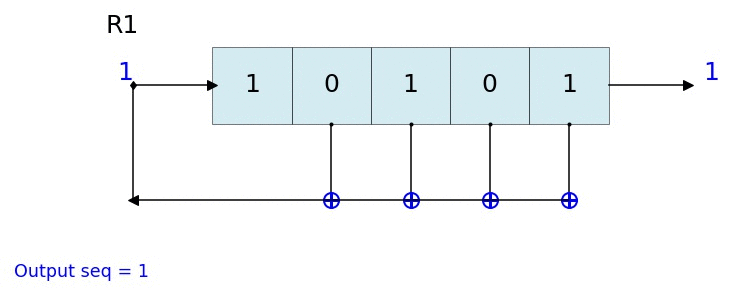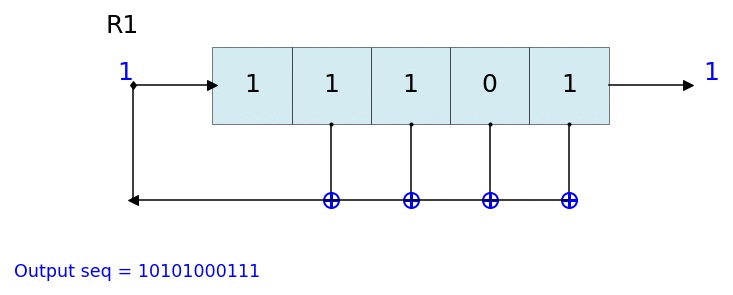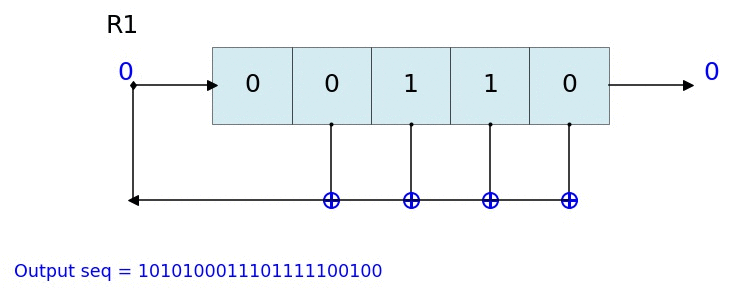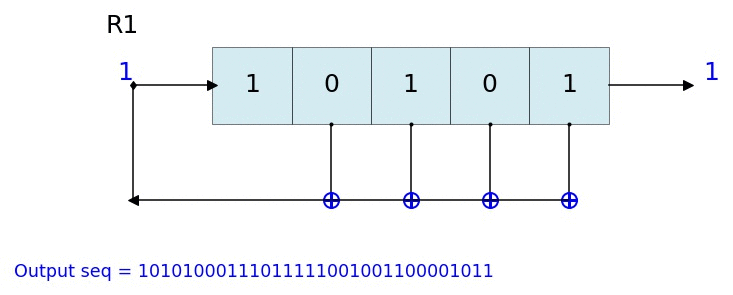
Example 5 ## 23 bit LFSR with custum state and feedback polynomial

fpoly = [23,19]
L1 = LFSR(fpoly=fpoly,initstate ='ones', verbose=False)
L1.info()

Output

23 bit LFSR with feedback polynomial  x^23 + x^19 + 1
Expected Period (if polynomial is primitive) =  8388607
Current :
 State        :  [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
 Count        :  0
 Output bit   :  -1
 feedback bit :  -1

seq = L1.runKCycle(100)

array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1,
1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0,
1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1])

Example 6 ## testing the properties

state = [1,1,1,1,0]
fpoly = [5,3]
L = LFSR(initstate=state,fpoly=fpoly)
result  = L.test_properties(verbose=2)

Output

1. Periodicity
------------------
 - Expected period = 2^M-1 = 31
 - Pass?:  True

2. Balance Property
-------------------
 - Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) =  (16, 15)
 - Pass?:  True

3. Runlength Property
-------------------
 - Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
 - Runs:  [8 4 2 1 1]
 - Pass?:  True

4. Autocorrelation Property
-------------------
 - Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
 - Pass?:  True

==================
Passed all the tests
==================

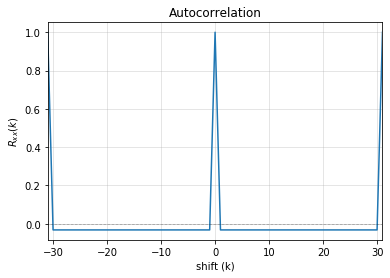
Testing individual property

# get a full period sequence
p = L.getFullPeriod()
p
array([0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0,
       0, 1, 0, 0, 1, 0, 1, 1, 0])

L.balance_property(p.copy())
# (True, (16, 15))

L.runlength_property(p.copy())
# (True, array([8, 4, 2, 1, 1]))

L.autocorr_property(p.copy())[0]
#True

Example 7 ## testing the properties for non-primitive polynomial

state = [1,1,1,1,0]
fpoly = [5,1]
L = LFSR(initstate=state,fpoly=fpoly)
result = L.test_properties(verbose=1)

Output

1. Periodicity
------------------
 - Expected period = 2^M-1 = 31
 - Pass?:  False

2. Balance Property
-------------------
 - Number of 1s = Number of 0s+1 (in a period): (N1s,N0s) =  (17, 14)
 - Pass?:  False

3. Runlength Property
-------------------
 - Number of Runs in a period should be of specific order, e.g. [4,2,1,1]
 - Runs:  [10  2  1  1  2]
 - Pass?:  False

4. Autocorrelation Property
-------------------
 - Autocorrelation of a period should be noise-like, specifically, 1 at k=0, -1/m everywhere else
 - Pass?:  False

==================
Failed one or more tests, check if feedback polynomial is primitive polynomial
==================

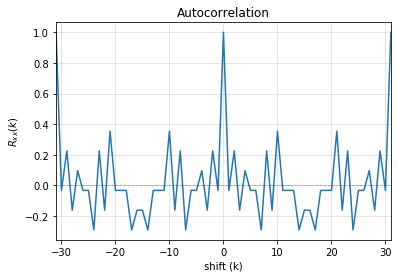
Example 8**: Get the feedback polynomial or list

Reference : http://www.partow.net/programming/polynomials/index.html

L = LFSR()
# list of 5-bit feedback polynomials
fpoly = L.get_fpolyList(m=5)

# list of all feedback polynomials as a dictionary
fpolyDict = L.get_fpolyList()

Changing feedback polynomial in between

L.changeFpoly(newfpoly =[23,14],reset=False)
seq1 = L.runKCycle(20)

# Change after 20 clocks
L.changeFpoly(newfpoly =[23,9],reset=False)
seq2 = L.runKCycle(20)

Generators

A5/1 GSM Stream cipher generator

Ref: https://en.wikipedia.org/wiki/A5/1

import numpy as np
import matplotlib.pyplot as plt
from pylfsr import A5_1

A5 = A5_1(key='random')
print('key: ',A5.key)
A5.R1.Viz(title='R1')
A5.R2.Viz(title='R2')
A5.R3.Viz(title='R3')

print('key: ',A5.key)
print()
print('count \t cbit\t\tclk\t R1_R2_R3\toutbit \t seq')
print('-'*80)
for _ in range(15):
    print(A5.count,A5.getCbits(),A5.clock_bit,A5.getLastbits(),A5.outbit,A5.getSeq(),sep='\t')
    A5.next()
print('-'*80)
print('Output: ',A5.seq)

A5.runKCycle(1000)
A5.getSeq()

Enhanced A5/1

Reference Article: Enhancement of A5/1: https://doi.org/10.1109/ETNCC.2011.5958486

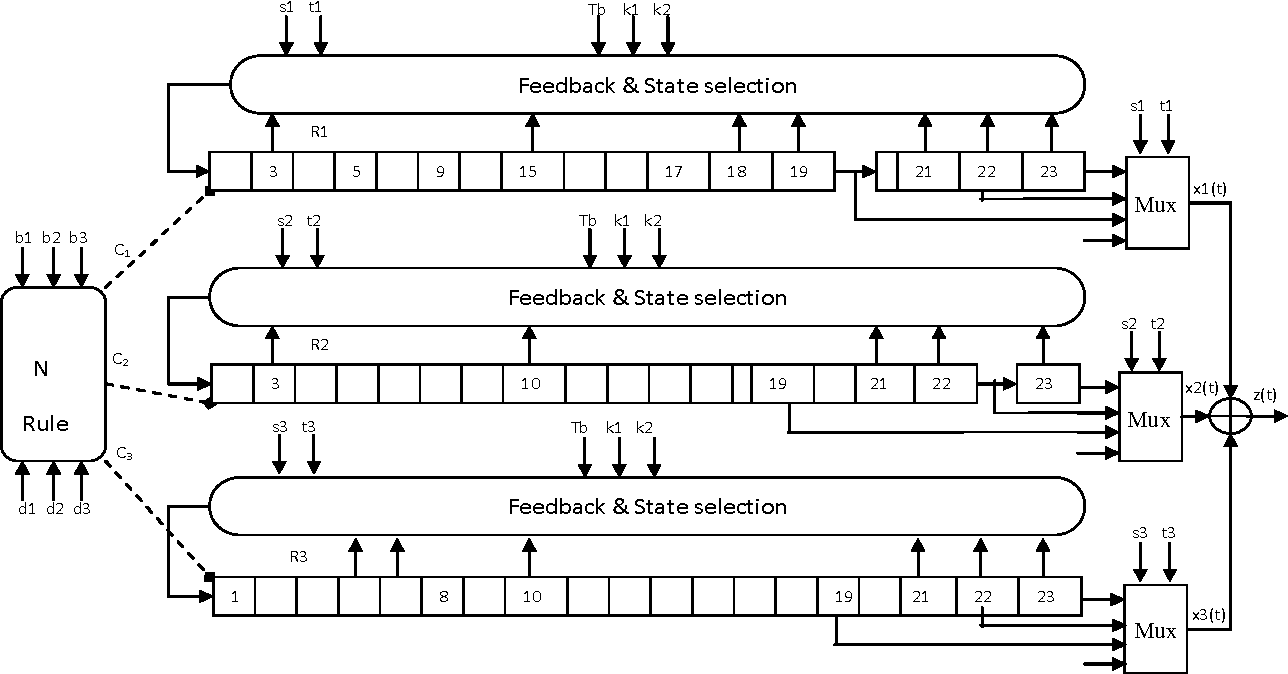
# Three LFSRs initialzed with 'ones' though they are intialized with encription key
R1 = LFSR(fpoly = [19,18,17,14])
R2 = LFSR(fpoly = [23,22,21,8])
R3 = LFSR(fpoly = [22,21])

# clocking bits
b1 = R1.state[8]
b2 = R3.state[10]
b3 = R3.state[10]

Geffe Generator

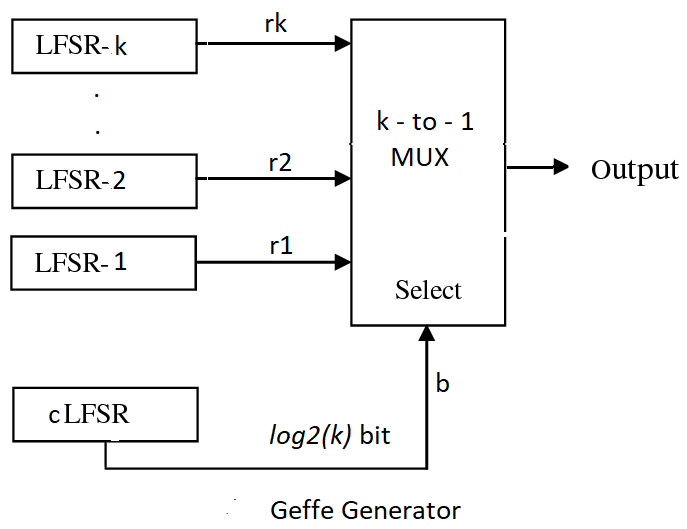
Ref: Schneier, Bruce. Applied cryptography: protocols, algorithms, and source code in C. john wiley & sons, 2007. Chaper 16

import numpy as np
import matplotlib.pyplot as plt
from pylfsr import Geffe, LFSR

kLFSR = [LFSR(initstate='random') for _ in range(8)]  # List of 8 5-bit LFSRs with default feedback polynomial and random initial state
cLFSR = LFSR(initstate='random')                      # A 5-bit LFSR with for selecting one of 8 output at a time

GG = Geffe(kLFSR_list=kLFSR, cLFSR=cLFSR)

print('key: ',GG.getState())
print()
for _ in range(50):
    print(GG.count,GG.m_count,GG.outbit_k,GG.sel_k,GG.outbit,GG.getSeq(),sep='\t')
    GG.next()

GG.runKCycle(1000)
GG.getSeq()

---

MATLAB

For matlab files download it from here

Folder : https://github.com/Nikeshbajaj/Linear_Feedback_Shift_Register/tree/master/matlabfiles

Description Genrate randon binary sequence using LFSR for any given feedback taps (polynomial), This will also check Three fundamental Property of LFSR

1. Balance Property
2. Runlength Property
3. Autocorrelation Property

This MATLAB Code work for any length of LFSR with given taps (feedback polynomial) -Universal, There are three files LFSRv1.m an LFSRv2.m, LFSRv3.m

LFSRv1

This function will return all the states of LFSR and will check Three fundamental Property of LFSR (1) Balance Property (2) Runlength Property (3) Autocorrelation Property

EXAMPLE

s=[1 1 0 0 1]
t=[5 2]
[seq c] =LFSRv1(s,t)

LFSRv2

This function will return only generated sequence will all the states of LFSR, no verification of properties are done here. Use this function to avoid verification each time you execute the program.

EXAMPLE

s=[1 1 0 0 1]
t=[5 2]
[seq c] =LFSRv2(s,t)

LFSRv3 (faster)

seq = LFSRv3(s,t,N) this function generates N bit sequence only. This is faster then other two functions, as this does not gives each state of LFSR

EXAMPLE

s=[1 1 0 0 1]  
t=[5 2]
seq =LFSRv3(s,t,50)

Tips

• If you want to use this function in middle of any program, use LFSRv2 or LFSRv1 with verification =0.
• If you want to make it fast for long length of LFSR,use LFSRv3.m

---

Cite As

@software{nikesh_bajaj_2021_4726667,
  author       = {Nikesh Bajaj},
  title        = {Nikeshbajaj/Linear\_Feedback\_Shift\_Register: 1.0.6},
  month        = apr,
  year         = 2021,
  publisher    = {Zenodo},
  version      = {1.0.6},
  doi          = {10.5281/zenodo.4726667},
  url          = {https://doi.org/10.5281/zenodo.4726667}
}

Contacts:

If any doubt, confusion or feedback please contact me

• Nikesh Bajaj
• http://nikeshbajaj.in
• n.bajaj@imperial.ac.uk
• n.bajaj@qmul.ac.uk
• bajaj[dot]nikkey[AT]gmail[dot]?

  PhD Student: Queen Mary University of London & University of Genoa

  ---

<!DOCTYPE html>

You will be redirected to https://pylfsr.github.io!

This site is open source. Improve this page.